leetcode1339. 分裂二叉树的最大乘积
给你一棵二叉树,它的根为 root 。请你删除 1 条边,使二叉树分裂成两棵子树,且它们子树和的乘积尽可能大。
由于答案可能会很大,请你将结果对 10^9 + 7 取模后再返回。
示例 1:
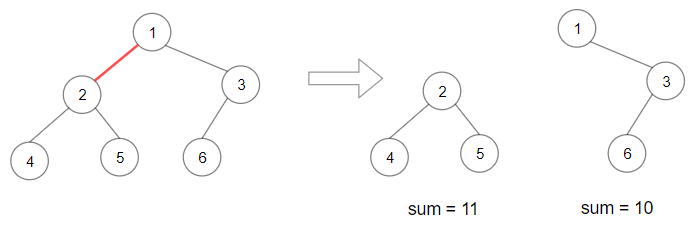
输入:root = [1,2,3,4,5,6]
输出:110
解释:删除红色的边,得到 2 棵子树,和分别为 11 和 10 。它们的乘积是 110 (11*10)
我最开始想到的方法是,便利整个树,每遍历一个节点,就求出他的子树和,这样就可以通过所有节点的和,求出来当前的max,max=(all-left)left.或者max=(all-rightright).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
long allNodeSum=0;
long max=0;
long mod=1000000000+7;
public int maxProduct(TreeNode root) {
allNodeSum=allNodeSum(root,0);
traverse(root);
return (int)(max%mod);
}
public long allNodeSum(TreeNode root,long sumSubtree){
if(root==null)return 0;;
long tmp=sumSubtree;
sumSubtree+=allNodeSum(root.left,tmp);
sumSubtree+=allNodeSum(root.right,tmp);
sumSubtree+=root.val;
return sumSubtree;
}
public void traverse(TreeNode root){
if(root==null)return ;
long left=allNodeSum(root.left,0);
max=Math.max((allNodeSum-left)*left,max);
long right=allNodeSum(root.right,0);
max=Math.max((allNodeSum-right)*right,max);
traverse(root.left);
traverse(root.right);
}
}
|
但是仔细想想,其实通过一次遍历就能解决.一次遍历,把当前节点对应的树的所有节点和求出来,然后放到一个list里面.这样最后只需要遍历一次list就可以了.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int maxProduct(TreeNode root) {
ArrayList<Long>list=new ArrayList<>();
long allNodeSum=allNodeSum(root,list);
long max=0;
long mod=1000000000+7;
for(long s:list){
if(s==allNodeSum)continue;
max=Math.max((allNodeSum-s)*s,max);
}
return (int)(max%mod);
}
public long allNodeSum(TreeNode root,ArrayList<Long>list){
if(root==null)return 0;;
long tmp=root.val+allNodeSum(root.left,list)+allNodeSum(root.right,list);
list.add(tmp);
return tmp;
}
}
|
leetcode 46/100